As in the Black-Scholes model for stock options and the Black model for certain interest rate options, the value of a European option on an FX rate is typically calculated by assuming that the rate follows a log-normal process.
In 1983 Garman and Kohlhagen extended the Black-Scholes model to cope with the presence of two interest rates (one for each currency). Suppose that rd is the risk-free interest rate to expiry of the domestic currency and rf is the foreign currency risk-free interest rate (where domestic currency is the currency in which we obtain the value of the option; the formula also requires that FX rates - both strike and current spot be quoted in terms of "units of domestic currency per unit of foreign currency"). Then the domestic currency value of a call option into the foreign currency is
The value of a put option has value
where :
- S0 is the current spot rate
- K is the strike price
- N is the cumulative normal distribution function
- rd is domestic risk free simple interest rate
- rf is foreign risk free simple interest rate
- T is the time to maturity (calculated according to the appropriate day count convention)
- and σ is the volatility of the FX rate.


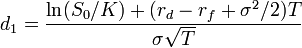

Tidak ada komentar:
Posting Komentar